空間の曲面
○空間内の曲面を数式で表現する方法として、まず、方程式F(x,y,z) = 0
によるものがあります。曲面が関数の
z = f(x,y)
のグラフになっている場合も
z - f(x,y) = 0
と書けるので、その特殊な場合と見なせます。
○もうひとつ、パラメータ表示によるものがあります:
p=p(u,v) (u,v)∈ D ⊂ R2
v を固定すると、p=p(u,v)は u をパラメータとする曲線になります。 これをu曲線といいます。逆に、u を固定すると、 p=p(u,v)は v をパラメータとする曲線になります。 これをv曲線といいます。
例: z = f(x,y) のグラフの場合は、 x=u, y=v とおけばパラメータ表示 p=(u,v,f(u,v)) が得られます。例えば z = x2+y2 の場合は、 パラメータ表示はp=(u,v,u2+v2) です。これを Maxima で描画したものが次の画像です:
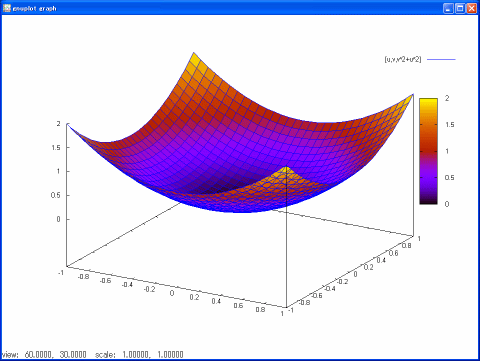
z=x2-y2の場合は次のようになります:
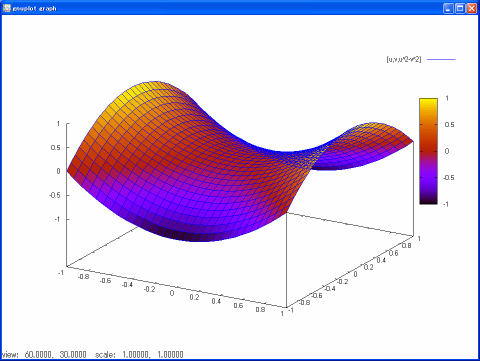
曲面の上に格子模様が描かれていますが、これらがu曲線やv曲線たちです。
u曲線の接ベクトルpu(=∂p/∂u)や v曲線の接ベクトルpv(=∂p/∂v)は、 ともに曲面の接ベクトルにもなっています。 pu(a,b)とpv(a,b) が 一次独立と仮定しましょう。するとこのふたつのベクトルは p(a,b)における曲面の「接平面」の基底で、 ベクトル積 pu(a,b)×pv(a,b) は 「法線ベクトル」を与えます。 ν(a,b)=pu(a,b)×pv(a,b) /|pu(a,b)×pv(a,b)|を 単位法線ベクトルといいます。
pu(u,v)やpv(u,v) はこれから重要な役割を 果たします。
パラメータ表示を与えることは、曲面上に「座標」(u, v) を導入することに他なりません。 例えば地球が半径1の球面であり、3次元空間の中で x2+y2+z2=1 という方程式で与えられているとします。 z軸の正の部分と球面の交点が北極、z軸の負の部分と球面の交点が南極と考えます。 z=0 の部分が赤道になります。 この球面の上の「座標」として、緯度 u と経度 v をとることにします(角の単位はラジアン)。 ただし、緯度 u は赤道上で0 、北極で π/2 、南極で -π/2とし、 経度 v は (1,0,0) の地点で 0 で、東に進むと大きくなり、西に進と小さくなるものとします。 -π/2≦u≦π/2、-π<v≦πの範囲で考えます。 このふたつの数値が与えられれば、球面上の1点が定まります。 残念ながら、北極と南極では経度 v が定まりませんが、あまり気にしないことにします。 ともかく「座標」(u,v) をもつ点は空間の座標を用いて表すと
p=(cos u cos v, cos u sin v, sin u)
となります(下図参照)。
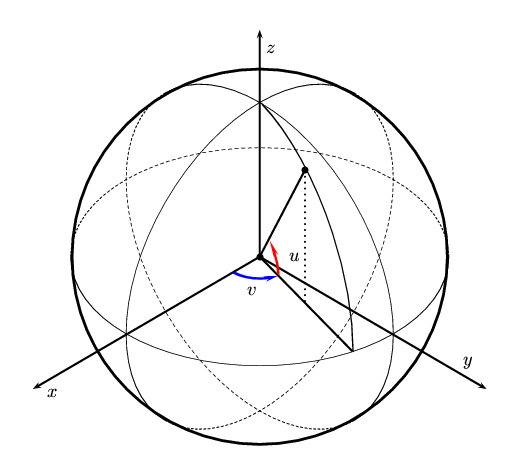
u曲線は、v を固定してえられる曲線ですが、v を固定するということは経度を 固定するということですから、得られるのは同じ経度を持つ点たち、すなわち ひとつの経線(半円周)になります。
v曲線は、u を固定してえられる曲線ですが、u を固定するということは緯度を 固定するということですから、得られるのは同じ緯度の点たちの作る曲線、 すなわちxy平面に平行な平面で切った円周になります。
演習
演習プリントNo.3を配布しました。 (a)では、そのパラメータに対応するu曲線、v曲線がどのようになるかも調べて、 図示してください。面倒ならば a=b=c=1 として構いません。