[目次]

幾何学II

■閉曲面のワード表示の変形

多角形（＝多辺形）の辺を２つずつ組にして貼り合わせたものは 閉曲面になりますが、その貼り合わせの指定を、「式」で表すこともできます。 頂点をひとつ決め、そこから時計回りに辺に与えられた文字を書き並べて いきます。ただし、辺に与えられた矢印の向きが時計回りならばそのまま 文字を書きますが、もし反時計回りならば文字の右肩に -1 をつけます。 このような式を「ワード（語）」と呼び、ワードによる閉曲面の表示を 「ワード表示」と呼びます。

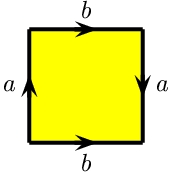
例： KBを図のように四辺形の辺を貼り合わせて表現する場合、左下の頂点から 出発すれば「abab-1」、左上の頂点から出発すれば、「bab-1a」、 右上の頂点から出発すれば「ab-1ab」、右下の頂点から出発すれば 「b-1aba」となります。

上の例のように、出発する頂点を取り替えても、文字の並びは「円順列」と解釈すれば 同じものになります。

前回、閉曲面 X, Y の連結和 X＃Y を定義しました。 Xが A というワードで表示され、Y が B というワードで表示されるならば、 X＃Y はその二つのワードを並べた AB というワードで表示できます。 ただし、A, B は共通の文字を持たないと仮定します。共通の文字があると、 並べたとき、同じ文字が４つ以上出てくるので困ります。 証明はすでに前回やりました。

例： P2＃P2のワード表示。
P2 のワード表示として cc というものがとれます。 もうひとつの P2 の表示を cc とすると、文字が重複してしまいますから、 例えば dd などとします。すると、P2＃P2 の表示として、 ccdd が使えることがわかります。以後面倒ですから、以上のことを次のように書くことにします：
　　　P2＃P2＝ cc ＃ cc ＝ cc ＃ dd ＝ ccdd


例： 以下の等式は、図の切り貼りでも証明できますし、 ワード表示における式変形でも証明することができます。
  1. KB ＝ P2＃P2
  2. T2＃P2＝P2＃P2＃P2 ＝KB ＃P2

注意：　連結和＃は定義しましたが、「引き算」は定義されていません。 従って、等式の両辺から同じものを引くことはできません。 例えば、上の２から「T2＝KB」などと結論してはいけません。

定義：一般にワード A ＝ ai0ε0 ai1ε1 …… aikεk （ただしεj＝±1）が与えられたとき、 その逆 A-1 を A-1 ＝ aik-εk …… ai1-ε1 ai0-ε0 と定めます。例えば、 (aba-1cd-1)-1 ＝ d c-1ab-1a-1 となります。

変形の基本

  1. 文字を取り替える。
    1. a → x, a-1 → x-1
    2. a → x-1, a-1 → x
  2. 巡回的に文字の並び方を変える：AB ←→ BA
  3. 隣り合う a と a-1 を取り去る。またその逆： A a a-1 B ←→ AB ←→ A a-1 a B
    ただし、AB は「空」ではないとする。
  4. Aa BC a-1 D ←→ A a' CB a'-1 D
    aB＝a' とおいて、その両辺に、形式的に右から B-1 をかけると、 a＝a'B-1という式が得られます。 さらに両辺の逆をとると、a-1＝B a'-1 が得られます。 これにより Aa BC a-1 D から a を消去するとA a' CB a'-1 D が得られます。この変形は実際に、aB という辺の集まりの端点を結ぶ線分(a')に 沿って多辺形を分割し、a で貼り合わせることと対応しています。 逆方向の変形も同様です。また a と a-1 の位置が入れ替わっている場合も 同様な変形が可能です。
  5. AB-1aaC ←→ Aa'Ba'C ←→ Aa"a"B-1C
    a'＝B-1a とおいて、両辺に左から B をかけると a=Ba' が得られます。 これをAB-1aaC に代入して a を消去すると、Aa'Ba'Cが得られます。 これも実際に多辺形を、縁の B-1a の部分の端点を結ぶ線分 a' で分割し、 a で貼り合わせることに対応しています。他の変形も同様です。
  6. 全体の逆をとる： A ←→ A-1
    これは多辺形を裏返すことに対応しています。


■課題： プリント：次回までの宿題です。用紙が不足する場合は、 裏を使ってください。それでも不足する場合は別の用紙に続きを書いて、ホッチキスで 留めてください。

※　11/7 は出張のため、休講です。

幾何学演習II

■単体の辺単体

n単体 σ＝＜v0, v1, ……, vn＞ の n+1 個の頂点の中から、k+1 個を選び出します：
　　　vi0, vi1, ……, vik
この k+1 個の点も一般の位置にありますから、これらを頂点とする k単体
　　　＜vi0, vi1, ……, vik ＞
を考えることができます。このようにして得られるk単体を、 σの 「k-辺単体」または「k-面単体」といいます。

辺＝1-辺単体＝1-面単体, 　　　面＝2-辺単体＝2-面単体　　　です。

n単体の k-辺単体の個数は n+1Ck+1 です。