幾何学II
■いろいろな図形(3)前回、正方形 I2={ (x,y)| 0≦x≦1, 0≦y≦1 }の辺を貼り合わせることにより、 新しい図形を作ることができることを学びました。
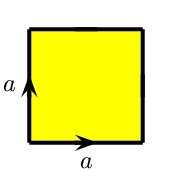
今回は次のような貼り合わせでどんな図形が得られるかを調べました。 左側のものは小テストとして取り上げました。
 |
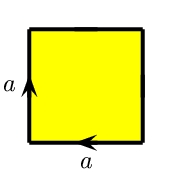 |
| 円板=正方形 | メビウスの帯 MB |
上のような問題を考える際には次のようなことに注意してください。
- つながっている所を切り離してはいけない。
- しかし、どうしても切り離す必要がある場合は、「印」をつけておいて、 あとで元のように貼り戻しておく。
右の貼り合わせではメビウスの帯MBができます。 印のついた2辺を分離するような対角線で、一度切り離してみるとわかりやすいです。
次に、クラインの壺や射影平面など3次元空間において実現できない図形を4次元空間で 実現するために、4次元空間の図形を表現する方法を学びました: 4次元空間を点(x,y,z,t)の全体と考え、t軸に直交する3次元空間で図形をスライスするという 「4次元版CTスキャン」により図形を表すことにします。 例えば「x2+y2+z2+t2=1」 で表される図形は「3次元球面」と呼ばれる図形です。 この図形をt=-1, t=-0.5, t=0, t=0.5, t=1 などの3次元空間で切ると、 それぞれ順に、一点、小球面、大球面、小球面、一点となります。
幾何学演習II
■辺単体
0≦k≦nとします。
n単体 σ=|v0 v1 …… vn| の
n+1 個の頂点の中から、k+1 個を選び出します:
vi0, vi1, ……, vik
この k+1 個の点も一般の位置にありますから、これらを頂点とする
k単体
|vi0 vi1 …… vik |
を考えることができます。このようにして得られるk単体を、
σの 「k辺単体」または単に「辺単体」といいます。
小テスト:2単体|v0 v1 v2|の辺単体をすべてみつけなさい。
n単体の辺単体の個数が 2n+1−1 であることを観察しました。
σの辺単体でσとは異なるものをσの「真辺単体」といいます。 σの真辺単体たちの和集合をσの境界といいます。 σから境界を取り除いたものをσの内部といいます。