[目次]

小テスト：|[1,2)∪[3,4]|=|[1,3]| であることを示せ。

■集合の濃度（続き）

前回「|A|=|B| ⇔ ∃f:A → B; 全単射」ということを学びました。 さらに濃度の大小関係を以下のように定めます：
　　　|A|≦|B| ⇔ ∃f:A → B; 単射
　　　|A|＜|B| ⇔ |A|≦|B| かつ |A|≠|B|

命題：A⊂B ⇒ |A|≦|B|

有限個の要素からできている集合を有限集合といいます。 そうでないとき、つまり無限に多くの要素をもつときは、 無限集合といいます。 A が無限集合であるとすると、 互いに相異なる要素の列
　　　a₁, a₂, a₃, a₄, ……
を作ることができます。この列は単射N → A を定めますから、 |N|≦|A| がわかります。

|A|＝|N|が成り立つのは、A が互いに相異なる無限個の要素たち
　　　a₁, a₂, a₃, a₄, ……
の和になるときです。そのような集合を可算(無限)集合といいます。 具体例は、N, Z, Q などがあります。 例えばZは、
　　　Z＝｛……, -3, -2, -1, 0, 1, 2, 3, ……｝
と、要素を一列に並べることができますが、可算集合であるという理由を説明するときは、 「先頭のある」列に並べ替えることが必要になります：
　　　Z＝｛ 0, 1, -1, 2, -2, 3, -3, ……｝
講義では有理数を一列に並べる方法を解説しました。

無限集合がすべて可算であるわけではありません。可算でない無限集合は 非可算(無限)集合とよばれます。

定理：R は非可算集合である。つまり、|N|＜|R|。

証明にはカントールの対角線論法を用いました。

自然数全体の集合 Nの濃度 |N| を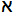 ₀と書きます。 また、実数全体の集合 Rの濃度 |R| を 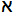と書きます。 この書き方を用いると上の事実は 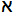₀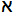＜ と表現することができます。

ここで出てきた不思議な文字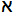はヘブライ文字のアレフです。 「アレフ」については、星野敏司さんの解説ページ http://www.nn.iij4u.or.jp/~hsat/techterm/aleph.html に筆順なども含んだ詳しい解説があるので、ぜひ読んでみてください。

まとめ：

1. 集合は、有限集合と無限集合の２種類にわかれる。
2. A が無限集合であるならば、必ず |A|≧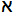₀ である。
3. 従って、無限集合はさらに
   • |A|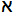＝₀のもの、つまり可算集合
   • |A|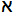＞₀のもの、つまり非可算無限集合
   の２種類にわけられる。

有限集合と可算集合をあわせて、高々可算な集合と呼ぶこともあります。

次の事実を知っていると便利です：
（ベルンシュタインの定理）　|A|≦|B| かつ |B|≦|A| ならば|A|＝|B|

あたりまえだと思ってはいけません。証明は面倒です。 詳しく知りたい人だけ、教科書で勉強してください。 講義では証明を省略します。

演習

小テスト：|N∪{0}| 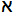＝₀ を示せ。

• 演習プリント No.3の９番を解きました。

他にも色々問題を解きました。下の問の(3)(4)(5)が残りました。

問　|A|＝|B| を示せ。（ベルンシュタインの定理を用いても良い）

1. A＝R−{0},　B＝(0,1)∪(2,3)
2. A＝Z,　B＝2Z＝｛……, -4, -2, 0, 2, 4, 6, ……｝
3. A＝[0,1],　B＝R
4. A＝R−{0},　B＝R
5. A＝R−{0},　B＝(-1, 1)