[目次]

幾何学II

■いろいろな図形(2)

前回に続いて、いくつかの２次元図形を紹介しました。 なお、我々が扱う２次元図形は「きれいな」図形のみです。 ここで、「きれいな」というのは、各点において、平面R2 あるいは半平面R2+＝｛(x,y)|y≧0｝ と同相（位相同型）な近傍が存在することを意味します （位相に関する専門用語は、数学要論IIの教科書で復習してください）。 「きれいな」図形 X において、平面と同相な近傍を持つ点のことを 「内部の点」、（半平面と同相な近傍はもつが）平面と同相な近傍を持たない点のことを、 その図形Xの境界点といい、境界点の全体 を ∂X と表します。

まず、次の３つはすべて互いに同相です。

講義では、E2からD2への同相写像を次の２つのステップで 作りました：

  1. ∂E2 から ∂D2 への同相写像を具体的に式で書く。
  2. 原点と境界の点を結ぶ線分を用いて、境界の間の写像を全体に拡張する。
  3. できた写像が連続な全単射であることをチェックする。
  4. 「コンパクト空間からハウスドルフ空間への連続な全単射は同相写像である」 という定理により、結果を得る。
次に、I2 の辺を貼り合わせることにより、いくつかの新しい図形を 導入しました：
円柱(シリンダー)
円環(アニュラス) A		 メビウスの帯 MB
 
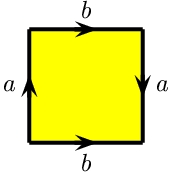
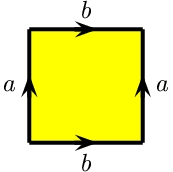
クラインの壷 KB トーラス T2 射影平面 P2

最後の射影平面は、aの辺とbの辺をつないで、cというひとつの辺にまとめると、 ２辺形の２辺を貼り合わせる形で表現できます：

　　　　　

この図形を３次元空間内に実現しようとすると、どうしても自己交差ができてしまいます。 そのような実現にはいくつか有名なものがあります。 ドイツのオーバーヴォルファッハ研究所には ボーイ曲面とよばれる実現の模型があります。 正直なところ、ぼくには一体どうなっているのかよくわかりません。 次回は射影平面を４次元空間の中に、自己交差なしに、実現してみます。 お楽しみに。

■課題：射影平面の中にはメビウスの帯が隠れています。 みつけましょう。また、その補集合（残り）はどんな図形ですか。
クラインの壺にもメビウスの帯が隠れています。こちらの方が見つけやすいでしょう。

幾何学演習II

■三角形の重心座標(2)

今回は、前回の問題を色々検討しました。

前回提出した次の課題は、レポート問題としました：

■課題： 三角形の外心、内心、垂心の重心座標を求めよ（頂角や辺の長さを使ってかまいません）。