幾何学II
■いろいろな図形(3)
今回は、まず次の小テストから始めました
■課題:クラインの壺の中にはメビウスの帯が隠れています。
みつけましょう。
メビウスの帯の貼り合わせ指定図を縦方向に縮めると、みつけやすくなります。
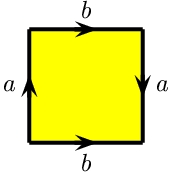 |
 |
| クラインの壷 KB | メビウスの帯 MB |
その「残り」をよく見ると、これがまたメビウスの帯になっていることがわかります。
つまり、クラインの壺はふたつのメビウスの帯を縁に沿って貼り合わせたものに
なっているのです。
これに、関連して、「普通の帯とメビウスの帯はどうやって見分ければよいのか」という 質問が出ました! 大変よい質問です。答えはいくつか考えられます。

- 帯の「片面」に色を塗ろうと試みる。もし「片面」だけに塗れたら、普通の帯。 もし、「裏側?」にまで塗れてしまったらメビウスの帯。
- 細い帯の図を書いたときに、「交差」の個数が偶数個なら普通の帯。 奇数個ならメビウスの帯。
- ふちをたどって見る。ふちが2本なら普通の帯。 1本につながっていたらメビウスの帯。
- 帯に住む双子の「生物」の兄が帯を一周して戻ってきたときに、
同じ場所で待っていた弟と「鏡映」の生物に変身していたらメビウスの帯。
そういうことがおきなければ普通の帯。「時計」で考えても同様。

ぜひ、実際に紙を使ってメビウスの帯や普通の帯を作って色々考えてみてください。
元々の課題は時間不足でできませんでした。次回、続けます。
■課題:射影平面の中にはメビウスの帯が隠れています。 みつけましょう。また、その補集合(残り)はどんな図形ですか。幾何学演習II
■三角形の重心座標(3)今回は、前回の問題を色々検討しました。
■課題: 三角形の外心、内心、垂心の重心座標を求めよ(頂角や辺の長さを使ってかまいません)。
その後、三角形ABCの中の点 X に対して、その重心座標がちゃんときまることを証明しました。 その際、「一次結合」「一次独立」「一次従属」などの概念の復習を行いました。 次回も続けます。