[目次]
■集合の濃度

要素の数が有限個の集合を有限集合、そうでない集合を無限集合といいます。 たとえば、N や R は無限集合です。

有限集合では、要素の個数は集合の区別をするのに役立ちますが、 無限集合では役に立ちません。 そこで、「個数」のかわりに「濃度」というものを用います。 集合Aの濃度は|A|という記号で表します。ただし、 濃度 |A| の定義は最終回まで、おあずけにします。 今回は、二つの集合の濃度の間の大小関係についてのみ説明します。

1. |A| ＝ |B|　⇔　∃f:A → B s.t. f は全単射
2. |A| ≦ |B|　⇔　∃f:A → B s.t. f は単射
3. |A| ＜ |B|　⇔　|A| ≦ |B|　だが　|A| ＝ |B|ではない

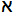自然数全体の集合 Nの濃度 |N| を ₀と書きます。 また、実数全体の集合 Rの濃度 |R| を 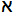と書きます。

ここで出てきた不思議な文字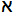はヘブライ文字のアレフです。 「アレフ」については、星野敏司さんの解説ページ http://www.nn.iij4u.or.jp/~hsat/techterm/aleph.html に筆順なども含んだ詳しい解説があるので、ぜひ読んでみてください。

さらに他のヘブライ文字に興味がある人は、 http://arabic.gooside.com/hebrew/kaki/kata.html がいいかもしれません。

次の事実は重要です：

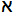1. ₀＜
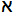
2. （ベルンシュタインの定理）　|A|≦|B| かつ |B|≦|A| ならば|A|＝|B|

１は次回証明します。２は興味のある方のみ、教科書で勉強してください。

演習

• プリント＃３ の1(1), 2(3), 7, 8を解きました。