[目次]
■集合の直積

集合 X, Y が与えられたとき、X の要素 x とY の要素 y のペア (x, y) を考えます。そのようなペア２つ (x, y), (x', y') に対し、
　　　　(x, y)＝(x', y') ⇔ x＝x' かつ y＝y'
とします。このようなペアを順序対といいます。 そのような順序対の全体を X×Y とかき、X と Y の直積といいます。
　　　　X×Y＝｛(x, y) | x ∈X かつ y ∈Y ｝
X × X は X² とも書きます。

問：|N×N|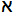＝₀ であることを示せ。

定義：写像 f:X → Y に対し、次の集合をそのグラフという：
　　　　Ｇ_f＝｛(x, f(x)) | x ∈ X ｝

■２項関係(1)

ある集合の要素 x, y に関する命題(関数) P(x,y) を X 上の２項関係とよびます。これを臨時に R であらわし、 P(x,y) が真であることを xRy と書くことにします。 例えば

数学では「＝」を用いた色々な関係が現れます。

• 集合の要素 x, y に関するもの：x＝y
• 順序対に関するもの：(x, y)＝(x', y')
• 集合に関するもの：X＝Y
• 写像に関するもの：f＝g

これらがそれぞれ同意味なのかきちんと理解して使っているでしょうか。 これらの関係には、三つの共通する性質があります：
　　　E1 (反射律) x ＝ x
　　　E2 (対称律) x ＝ y ⇒ y ＝ x
　　　E2 (推移律) x ＝ y かつ y ＝ z ⇒ x ＝ z

そのような関係を「同値関係」と呼びます。つまり、 一般に集合X上の関係Rが次の条件を満たすとき、同値関係といいます：
　　　E1 (反射律) x R x
　　　E2 (対称律) x R y ⇒ y R x
　　　E2 (推移律) x R y かつ y R z ⇒ x R z

集合の上の（一般の）同値関係はしばしば「〜」の記号で表されます。

例：

• 平面図形の間の合同という関係 A ≡ B は同値関係です。
• 平面図形の間の相似という関係 A ∽ B は同値関係です。
• 実数の間の「以上」という関係 x ≧ y は同値関係ではありません。
• 実数の間の「x²＋y²＝1」という関係は同値関係ではありません。
• 整数の間の「p を法とした合同　x ≡ y (mod p) 」は同値関係です。 ただし、上の式は「x − y が p の倍数である」ことを表しています。

定義　集合 X の上の同値関係〜が与えられているとき、各 x ∈ X に対し、
　　　　C(x)＝｛ y ∈ X | y 〜 x ｝
を x の同値類といいます。

演習

色々な例で「同値類」がどんな集合になるか調べました。