最初に、教科書 p.23 例題1.8の(1)、p.24 定理 1.3 の(1) などを解きました。
■集合の濃度
n個の要素からなる集合 A に対し、#A = n と定めます。 つまり #A は集合 A の要素の個数です。無限個の要素をもつ集合 A に対しては、 #A =∞ とは定めません。では、どう定義するのか……それは次週にまわすすことにして、 次のような「関係」のみを定めることにします。
定義: 2つの集合 A, B の「濃度」 #A, #B の関係を次のように定める;
- #A = #B ⇔ ∃f : A → B ; 全単射
- #A ≦ #B ⇔ ∃f : A → B ; 単射
- #A < #B ⇔ #A ≦ #B かつ #A ≠ #B
次の定理は便利です:
ベルンシュタインの定理
#A ≦ #B かつ #B ≦ #A ならば #A = #B である。
これは当たり前ではありません。興味のある人は、夏休みに教科書の証明を読んでみてください
(p.63, p.64)。
自然数全体の集合の濃度 #N, 整数全体の集合の濃度 #Z,
有理数全体の集合の濃度 #Q, 実数全体の集合の濃度 #Rに関して、
つぎのような関係が成り立つことを観察しました:
#N = #Z = #Q < #R
#N のことを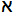 0,
#R のことを
0,
#R のことを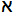 と書きます。
と書きます。
演習問題No3の5,6,9(1)(2) などを解きました。
模擬試験問題その1を配布しました。