[目次]

---

幾何学II

■いろいろな図形(1)

前期の幾何学Iで、曲線や曲面などの図形は

1. 方程式
2. パラメータ表示

などによって表現できることを学びました。 パラメータ表示に必要なパラメータの個数をその図形の次元とよびます。 後期の幾何学IIでは、それら以外の方法も学びます。 最初の２回の講義で、これから扱うことになるいろいろな図形を紹介します。

１次元の図形

数直線 R

円周 S¹ ： ｛ (x,y) ∈ R²| x²+y²=1 ｝

２次元の図形

座標平面 R²

２次元球面 S² ： ｛(x,y,z) ∈ R³| x²+y²+z²=1 ｝

３次元の図形

座標空間 R³

３次元球面 S³ ： ｛(x,y,z,t) ∈ R⁴| x²+y²+z²+t²=1 ｝

３次元球面を「見る」方法にはいくつかあります。 映画のフィルムのように「動画」を用いる方法について解説しました。 詳しくは昨年度のページをご覧ください。

---

幾何学演習II

■三角形の重心座標(1)

三角形に関する「チェバの定理」と「重心座標」について学びました。

平面の線分AB上の点Pに対する次のような公式（高校で学ぶ）を復習しました。 ただし、s_A, s_B は各線分の長さを表します。

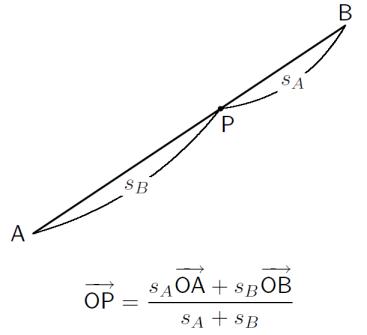
平面の三角形ABCの中の点Pに対する次のような公式を紹介しました。 ただし、s_A, s_B, s_C は各小三角形の面積を表します。

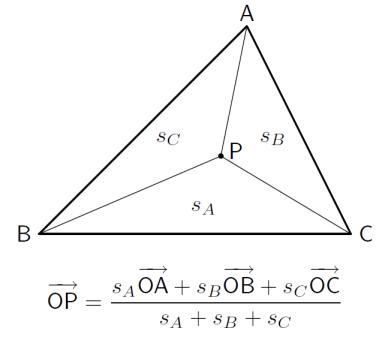
証明は演習問題にしました。次回、黒板で説明してもらいます。 チェバの定理の証明がヒントになるでしょう。

三角形ABCの中の点Pに対し、

• α＝s_A/(s_A+s_B+s_C)
• β＝s_B/(s_A+s_B+s_C)
• γ＝s_C/(s_A+s_B+s_C)

とおきます。α＋β＋γ＝１が成り立ちます。 （α, β, γ）のことを△ABCにおけるPの重心座標と呼びます。 例えば、どんな三角形でも重心Ｇの重心座標は(1/3, 1/3, 1/3)です。

課題：三角形の外心、内心、垂心の重心座標を求めよ（頂角や辺の長さを使ってかまいません）。