[目次]

---

幾何学II

■前回の訂正および補足
訂正：こちら
変形についての補足
(1)(2)(3)に変形する場合、次の事実を用いることもできます：

事実： X 〜 X', Y 〜 Y' （同相）＝＝＞ X ＃ Y 〜 X' ＃ Y' （同相）

使用例：　c c a^-1 b^-1 e f e^-1 f^-1 a b 〜 P² ＃ P² ＃ P² ＃ P² ＃ P²

　　　c c a^-1 b^-1 e f e^-1 f^-1 a b
　＝　P² ＃ a^-1 b^-1 e f e^-1 f^-1 a b
　〜　P² ＃ e f e^-1 f^-1 a b a^-1 b^-1　　　　※
　＝　P² ＃ T² ＃T²
　＝　（P² ＃ T²） ＃T²
　〜　（P² ＃ P² ＃ P²） ＃T²　　　※
　＝　（P² ＃ P²） ＃ （P² ＃T²）
　〜　（P² ＃ P²） ＃ （P² ＃ P² ＃P²）　　　※
　＝　P² ＃ P² ＃ P² ＃ P² ＃ P²

※のところで上の事実を用いています。

■閉曲面のセル分割

セル複体（ただし２次元以下）の概念を導入しました。 単体複体は単体の集まりですが、セル複体は「セル」の集まりです。

• 0セルは空間の点です。0単体と同じものです。 有限個の0セルがあるものとしましょう。
• 1セルは線分の端点を、すでにある0セルに貼り付けたものです。 （これも有限個とします）
  • 1セルはまがっていてもかまいません。
  • ひとつの1セルの両端が同じ0セルに貼り付けられてもかまいません。
  • 1セルは端点以外の点で0セルや1セル（自分自身や他のもの）にぶつかってはいけません。
• 2セルは円板（またはそれと同相な図形）のふちを、すでにある 0セルや1セルに貼り付けたものです。（これも有限個）
  • 2セルはまがっていてもかまいません。
  • ふちはつぶれたり、異なる点が同じところに貼り付けられてもかまいません。
  • 2セルはふち以外の点で0セルや1セルや2セル（自分自身や他のもの） にぶつかってはいけません。

定義：　K がセル複体であるとき、K のセルの和集合を K の表す図形 と呼び、|K| とかきます。

定義：　図形 X に対し、|K| 〜 X （同相）となるセル複体とその同相写像の ペアをXのセル分割といいます。

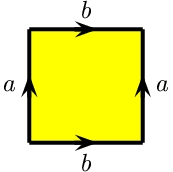
例：　閉曲面の2n辺形の辺の貼り合わせによる表示は、閉曲面のセル分割を与えます。 例えば下の図はトーラス T² の、ひとつの0セル、２つの1セル(a と b) 、 ひとつの2セルからなるセル分割を与えます：

---

幾何学演習II

■単体複体の鎖複体(1)

単体に「向き」の概念を導入し、「i鎖」の概念および線形空間 C_i(K;R) を定義しました。 詳しくはkika2i.pdfをご覧下さい。 講義と若干異なる定義を用いていますが、本質的に同じです。

■小テスト
<a,b,c,d> と <b,c,d,a> は向きのついた3単体と考えたとき、 同じになるか逆になるか。